The Journal of Credibility Assessment and Witness Psychology

2002, Vol. 3, No. 1, pp. 1-22

Published by the Department of Psychology of Boise State University

P300 Scalp Distribution as an Index of Deception: Control for Task Demand

J. Peter Rosenfeld, Archana Rao, Matthew Soskins,

& Antoinette Reinhart Miller

Northwestern University, Department of Psychology

Correspondence regarding this article should be addressed to Dr. J. Peter Rosenfeld, Department of Psychology and Institute for Neuroscience, Northwestern University, 2029 Sheridan Rd., Evanston, IL 60208. EMAIL: jp-rosenfeld@northwestern.edu

---

Copyright 2002 by the Department of Psychology of Boise State University and the Authors. Permission for non-profit electronic dissemination of this article is granted. Reproduction in hardcopy/print format for educational purposes or by non-profit organizations such as libraries and schools is permitted. For all other uses of this article, prior advance written permission is required. Send inquiries by hardcopy to: Charles R. Honts, Ph. D., Editor, The Journal of Credibility Assessment and Witness Psychology, Department of Psychology, Boise State University, 1910 University Drive, Boise, Idaho 83725, USA.

---

 ABSTRACT: Participants (n=24) experienced a baseline Block 1: they saw their phone numbers presented in a series with 6 other phone numbers. They were to say “yes” to their phone numbers, “no” to others. They were asked to repeat the first 3 digits of the phone numbers aloud. In Block 2, LIE and CONTROL groups (both n=12) were formed: participants saw a series of dates (e.g., “Mar 9”), 14% of which were their birth dates. The LIE participants were asked to lie on 50% of the trials, and to repeat all stimuli aloud. The CONTROLs were to perform honestly in Block 2, and were asked to repeat all stimuli aloud, but a random half of the stimuli backwards. The aim was to equalize task demand between groups. The results were that for both scaled and unscaled P300 amplitude, there were no differences or interactions as a function of group, or block in comparisons of responses to honest, forwards-repeated stimuli (p>.6). For pooled Block 1-Block 2 honest responses vs Block 2 dishonest responses in the LIE group, there was a main effect of response type on unscaled amplitude (lie responses<true responses, p<.03). Conversely, there was no main effect in the CONTROL group of the forwards/backwards manipulation (p>.15). In scaled amplitudes, there were no interactions of group or response type with site (p>.2) in honest, forwards responses. Comparing all scaled LIE honest with dishonest responses in the LIE group yielded a significant interaction of response type x site, p<.02. Post-hoc ANOVAs, using just Cz and Pz showed a significant interaction in the LIE but not CONTROL participants. There were no P300 latency differences between groups or conditions. In an extended replication, reaction time data did not differ between LIE and CONTROL groups. The results continue to support the notion that a P300 profile, specific for deception, may be identifiable. 

---

P300 Scalp Distribution as an Index of Deception: Control for Task Demand

Introduction

We have previously reported that in various situations, the scaled scalp distribution (profile) of P300 amplitude differs from deceptive to truth-telling conditions, (Rosenfeld, Reinhart, Bhatt, Ellwanger, Gora, Sekera, & Sweet, 1998; Rosenfeld & Ellwanger, (1999), Rosenfeld, Ellwanger, Nolan, Wu, Berman, & Sweet, 1999). Johnson (1988, 1993) has argued that when the ERP profile differs from one condition to another, this is good evidence that the two conditions involve differing neurogenerator groups.

Although one may take advantage of differential profiles for truth-tellers and liars in practical detection of deception applications, one cannot argue from such data that the liar’s profile specifically represents deception. In the paradigms previously used (Rosenfeld & Ellwanger, (1999); Rosenfeld et al, (1999); Rosenfeld et al., 1998), the task demands on the liar were greater than those on the truth-teller: The latter simply had to tell the truth whereas the liar had to maintain an instructed, random-appearing, 50% (approximately) deceptive error rate, and thus also had to decide on each trial whether or not to lie. The observed differences in profile between the two groups could have represented differences in task demand as well as differences in honesty.

In the present study, we tried to construct an honest control group having task demands comparable to those of the liar group. Specifically, we used an autobiographical oddball paradigm in which participants saw a Bernoulli (randomized) series of seven, repeatedly presented dates, 14.3 percent of which were their own birth dates. In the Lie group, participants were told to respond dishonestly on a random half of the trials (of both oddball and frequent type), and to then repeat the stimuli aloud. (Only the first three letters of the month were repeated.) In the Control group, participants were told to respond aloud honestly on all trials, but to then repeat a random half of the stimuli aloud backwards, (the rest, forwards). Both groups had comparable task demands in the terms noted above, but one group responded honestly and the other dishonestly. Differing P300 profiles would not be simply attributable to differences in task demands.

In this study, there is a second set of evidence examined which bears even more directly on putative specificity of Lie profiles: On the block of trials where the Lie participants respond dishonestly on half the trials, there is the opportunity to compare the P300 profiles associated with honest and dishonest response trials. Since task demands are the same during the entire block within the Lie group, obtained profile differences would provide support for the specificity hypothesis. We looked for but failed to find such an effect earlier (Rosenfeld et al., 1999) using a different (match-to-sample) paradigm.

We note that Johnson’s (1988, 1993) interpretation of the meaning of differing scalp profiles emphasizes the possibility of differing neurogenerator sets. There is another interpretation of the differing scalp profiles in two experimental conditions: It may be that the two conditions evoke different sets of components which differentially overlap the P300 which both conditions evoke in common (Donchin, Spencer, & Dien, 1997). Either interpretation implies that the brain works in a specific way during deception, and the evidence would become the first to support a specific lie response, said to be a “dream” by Lykken (1981). Such a finding would also be a step in the direction of elucidating brain systems involved in lying.

Why might one expect differing scalp distributions in Lie and Control groups if task demand is matched? We hypothesize that a participant who is lying, even though he/she was directed to do so, has some level of self-awareness on all deceptive trials; that he/she is engaging in a behavior on which society and authority figures frown. At least some participants may thus find themselves somewhat embarrassed at being observed during lies. More important, all Lie participants (and no Control participants) know they are lying as they lie, and probably engage in further lie-specific cognitions following the decision to lie as well as following the act of lying. These cognitions would pertain to knowledge of the mismatch between the true-correct answer versus the answer they produce on a lie trial. We hypothesize that the Lie condition, but not the Control condition, will generate brain activity related (at least) to both the additional cognitions following such mismatch experiences, as well as to self awareness of deception, and that P300 profiles may reflect these differences between Lie and Control conditions.

Differences between Lie and Control groups might also be expected on the basis of the latter’s additional task: backwards repetition of stimuli. A comparison restricted to profiles of Lie and Control groups during their respective specific tasks could thus be confounded by the two task effects simultaneously operating: 1) honest vs. dishonest responding and 2) backwards vs. forwards repetition. We therefore ran both groups through two blocks of trials, one (Block 1) in which all participants behaved alike in responding honestly and repeating stimuli forwards, and a second block (Block 2) in which the Lie participants lied on half the trials with forwards repetition, and the Control participants responded honestly on all trials but repeated half the stimuli in a backwards manner. Thus in each group, we could compare departures in Block 2 from the benchmark/baseline condition of Block 1.

Method

Participants: The 24 participants (12 per group, 13 female, six of which were in the Lie group) were recruited from the department introductory psychology pool and were fulfilling a course requirement. All had normal or corrected vision.

Procedure: Following signing of consent form, instruction, and electrode attachment, participants were seated in a recliner such that a video display screen was in front of their eyes. The visual stimuli were presented on this screen every 6.0 s, a relatively long interstimulus interval required for verbal responding so as to allow the artifact associated with vocalization to dissipate prior to the subsequent trial. The trial began with the onset of pre-stimulus EEG baseline recording for 104 ms. The stimulus then appeared on the screen and endured for the remainder of the ERP recording epoch = 1944 ms (total epoch = 2048 ms). Immediately after clearance of the stimulus from the screen, the message "Please Respond" was presented and lasted 2 s. The participant was required to respond during this time.

There were two blocks of trials used in this study. In the first block (Block 1), the visual stimuli were participants’ phone numbers (p = .14) and other phone numbers (p = .86), each repeated as many times(about 40) as the subject’s phone number. Both Control and Lie participants were told to respond aloud truthfully and ordinarily in this preliminary block. The timing and parametric settings in this benchmark/baseline block were the same as in the actual test block (2) to be next detailed. In this second block (Block 2), the stimuli were the first three letters of a month, followed by a number from 1 to 31, e.g., MAR 9. Thus, birth dates could be formed. The participant then said "yes" or "no" signifying birth date or other date, respectively, and then immediately repeated aloud the three-letter symbol of the month.

In the Control group, the participants were (in Block 2) instructed to respond honestly "yes" or "no" and to then repeat these month symbol letters aloud backwards on approximately half the trials of both types (birth date, non-birth date). They were also instructed to try giving a random, as opposed to patterned, series of forward and backward responses. We suggested to these participants that we were interested in how well people can generate random sequences of responses while doing a foreground task. We also alerted them that if the computer detected patterned responding, the experiment would be re-started.

In Block 2, the Lie group participants were instructed to simulate malingered cognitive deficit as in Rosenfeld et al. (1998), by making dishonest "errors" on both trial types about half the time in response to the "Please Respond" message. They were told to generate a random, unpatterned series of deceptive responses, since the computer controlling the experiment could discern patterns, and that they would not "beat the test" if patterned responding was discerned, and the experiment would be re-started. Immediately after their "yes" or "no" response, they were required to repeat the first three letters of the month (in the normal, forwards order). Both groups were told there would be 45 presentations of birth dates randomly interspersed among 276 presentations of other dates; i.e., six dates each repeated 45 times. This was done in order to help them score close to the 50% target rate of deceptive or backwards responses. Following the response window (2.0 s) was a second 2.0 s period of no events prior to the start of the next trial. (Verbatim instructions are available on request from the senior author.) Table 1 presents stimulus-response combinations for both groups and both blocks, with abbreviations.

EEG recording and analysis: EEG was recorded with Grass P511k preamplifiers with gain = 100,000, and filters set to pass signals between 0.1 and 30 Hz (3db points). Electrodes (Ag - AgC1) were attached to Fz,Cz, and Pz referenced to linked mastoids with the forehead grounded. Impedances were maintained below 5000 ohms. EOG was recorded from a bipolar pair of electrodes above and below the eye. EOG signals > 80 uV led to trial rejection and replacement. Amplified signals were led to 12-bit A/D converters (Keithley-Metrabyte) sampling at 125 Hz, and the digitized signals led to a computer for on-line sorting, averaging, and storage. The computer programs (by the senior author) also controlled stimulus presentation, and performed off-line filtering and analyses.

In the present study, P300 determination is based on a standard baseline-to-peak method: The computer searches within each participant's average ERP within stimulus, paradigm and response categories (see Table 1), within a window which extends from 400 to 1000 ms post-stimulus for the 104 ms segment average (13 data points) which is most positive-going. From this segment average, the average of the first, pre-stimulus, 104 ms of the recording epoch is then subtracted. The difference defines unscaled P300 amplitude.

The midpoint of the maximally positive segment defines P300 latency. This is a typical method of measuring P300 (Fabiani, Gratton, Karis, & Donchin, 1987).

The method just described is done only with Pz recordings. For the Cz and Fz sites, the temporal boundaries of the maximally positive segment at Pz are used to define the window over which P300 amplitude is calculated. This procedure is utilized to be certain that the same neural process is sampled across sites for purposes of profile construction. It is typically used by researchers who focus on scaled P300 amplitude profiles (e.g. Ruchkin, Johnson, Grafman, Canoune, & Ritter, 1992).

For group analyses, P300 latency and amplitude were based on unfiltered averages for each participant. For display, averages were digitally filtered to pass low frequencies; 3db point: 4.23 Hz. For task-by-site interactions, average P300 amplitudes within each participant were filtered and then scaled using the vector length method (McCarthy & Wood, 1985): Within each group and/or stimulus/response condition, the average Fz, Cz, and Pz values for the condition/group were squared, and the square root of the sum of the squared values was used as a denominator by which individual Fz, Cz, or Pz values within the condition/group were divided.

It is noted that analyses are performed here on both scaled and unscaled data. To look at main effects of group, stimulus type, block, response type, and scalp site on amplitude, it is appropriate to look at unscaled data (McCarthy & Wood, 1985). However, to answer questions involving interactions with site, (the major questions here) McCarthy & Wood (1985) explained the need for analysis on scaled data. What the scaling accomplishes is the removal of possible amplitude differences between conditions, which may confound amplitude distribution differences. The scaling procedure in the present study removes main effects of group, paradigm, response type, and stimulus type, and allows meaningful interpretation only of interactions involving site. Thus, as recommended by McCarthy & Wood (1985), we report analyses on both scaled and unscaled data, as appropriate. (Latency need not be scaled).

Extended Replication: The above procedures were repeated one year later, with one modification, on two new groups of Lie and Control subjects, (N=10, 11 respectively): Interspersed randomly among the oddball and frequent trials were 20 probe trials. On these trials, the word “Go” appeared on the computer screen and all participants were instructed to press a response button as soon as possible thereafter. This allowed us to obtain reaction time (RT) data and compare RTs between Control and Lie groups. Such information could then support our contention of equalization of task demands between groups; (RT is frequently used to assess task demand.) The probe trial stimuli appeared with the same timing as the other stimuli. Although electrodes were attached as in the original study and ERPs recorded, the ERP analysis presented is based on the original experiment. The modified replication was analyzed here only for RT data.

Results

Note: The key quantitative results on scaled data are in sections E and F below, and in Figure 6. Other results are reported immediately below in sections A, B, C, and D.

A. Behavioral (original study): The mean numbers of responses in each stimulus-response category (see Table 1 for abbreviations) are shown in Table 2. There are six rows in each group and the numbers in the first row in the Lie group should correspond to those in the first row in the Control group, the second row in the Lie group with the second row in the Control group, and so on. The appropriate correspondences are close except for the fifth (second to the last) row, involving frequent stimuli (Lie = 101.58 vs. Control = 87.75). For the first four rows involving the oddball responses in both groups in both blocks, and the frequents of Block 1, there were no significant differences.

Table 2: Average numbers (+ SEM) of responses in each possible stimulus-response category. Table 1 and text define category abbreviations.
Row Lie Group	Category	Number
1	OD1[L]	24.67 +/- .97
2	FR1[L]	146.58 +/- 5.80
3	OD2-TRU	17.25 +/- .85
4	OD2-LIE	15.00 +/- .90
5	FR2-LIE	101.58 +/- 4.46
6	FR2-TRU	86.50 +/- 4.24
Control Group
1	OD1[C]	25.67 +/- .99
2	FR1[C]	143.67 +/- 7.16
3	OD2-FOW	15.17 +/- .91
4	OD2-BAC	14.83 +/- 1.28
5	FR2-BAC	87.75 +/- 6.54
6	FR2-FOW	87.80 +/- 5.26

There were significant effects regarding the last two rows containing frequent stimulus data, however these will not be detailed since all ERP analysis will focus only on oddball trials; P300s in many participants on frequent trials in both groups were dubious. The present behavioral data indicate comparability between groups for oddball stimulus-response combinations; (the differences found for frequents were small though significant).

B. RT data (modified replication): Average RTs to probe stimuli within each subject were averaged to yield separate group means, for each of the two blocks. For the first block in which all subjects performed in the same manner, the mean RT (+/- SD) for the Control group was 1.109S (+ .3984) and for the Lie group was 1.305S (+ .2098). On this difference, t(19) = 1.425, p = .17 (ns). In the critical second block, the differences were similar: Control = 1.02 S (+ .3925), Lie = 1.221S (+ .1927); t(19) = 1.47, p = .16 (ns). These negative data suggest that the two tasks did not impose differential demands on the two groups of subjects.

C. ERP data: Qualitative observations in grand average ERPs: In the first block, there should be no ERP differences between groups in response to either oddball or frequent stimuli, since both Lie and Control groups are behaving exactly alike in this block (see Table 1 and methods). Differences between groups in amplitude and latency of P300 did not, in fact, reach significance (see below).

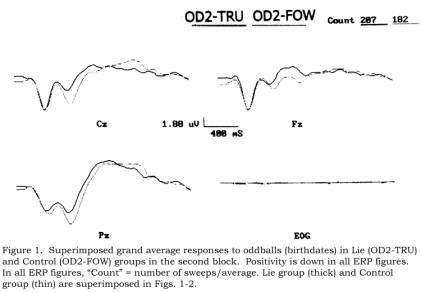
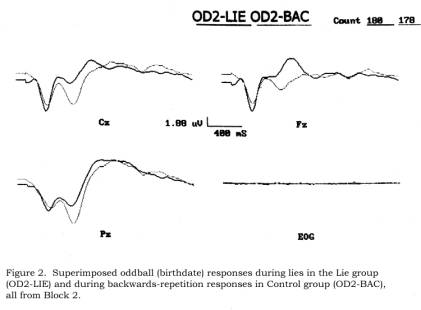
For quality control purposes, Figure 1 shows superimposed Lie and Control grand averages for OD2-TRU and OD2-FOW trials (all honest, forwards responses in block 2). It appears that the P300 is reduced in the Lie group relative to the Control group. Figure 2 shows superimposed Lie and Control grand averages for OD2-LIE (dishonest, forwards) and OD2-BAC (honest, backwards) trials, and again, the P300s appear larger in the Control group.

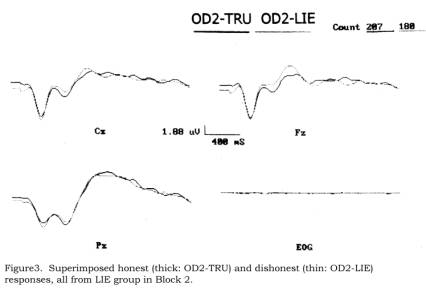
Figure 3 shows superimposed OD2-TRU (honest) and OD2-LIE (dishonest) responses within the Lie group. The former set appears to have more positive P300 responses, especially at Fz and Cz. (The differences would be more obvious if we chose, in the figures, to superimpose pre-stimulus baselines, which our P300 calculation algorithm does do. 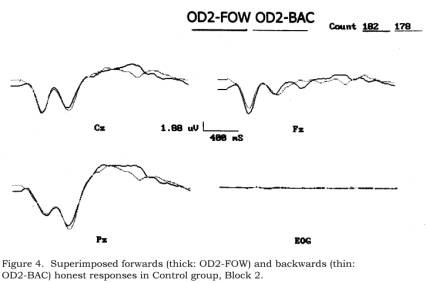We present data in figures as they really are, i.e., with random-noise related baseline shifts.) In Figure 4, comparable superimpositions are shown within the Control group: OD2-FOW (forwards) vs. OD2-BAC (backwards). In this comparison, P300 in the latter category appears slightly more positive (which, again, would be more evident with aligned baselines).

D. P300 amplitude data analysis: Unscaled data: We restrict reporting of results to oddball trials, since it was frequently impossible to locate a clear P300 peak in the frequent averages within participants.

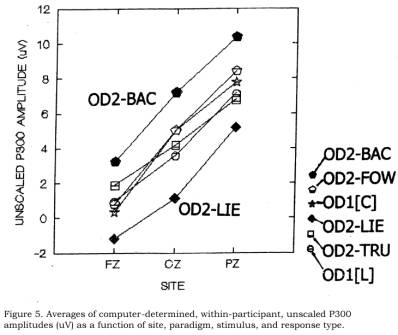
Figure 5 shows the group average, computer-determined P300 amplitude values as functions of site, group, block (1 vs 2), and stimulus-response combination. It appears that within the Lie group, there is little difference in amplitude or slope, between OD1-[L] and OD2-TRU amplitudes (both associated with honest responses), but that lying (OD2-LIE) produces a depression of amplitudes. In the Control group, the OD1[C] and OD2-FOW response curves are also aligned, and indeed do not appear to differ from comparable Lie group honest response curves just described. This is as predicted. However, in the Control group, the OD2-BAC amplitudes appear enhanced by the backward condition manipulation.

To obtain statistical confirmation of these effects, we first examined possible group and block differences during honest, forwards responses OD1[L], OD2-TRU, OD1[C], OD2-FOW. The sets of P300 amplitudes classified in this way were submitted to a 3-way ANOVA, with independent variables group (Lie vs. Control), site, and Block (1 vs. 2 for both groups).

The effect of group was not significant (p >.7). Neither was the effect of Block (p >.6). The effect of site yielded F(2,44) = 134.34, pg < .001 (pg is the Greenhouse-Geiser corrected probability in within-subject tests with df > 1. The correction is for sphericity effects. For df = 1 tests, the usual p-values will be reported.) The interactions were not significant, (p >.2), excepting the group-by-site interaction, which yielded F(2,44) = 4.18, pg < .04, reflecting the somewhat steeper slopes for honest, forwards Control curves than for the honest, forwards Lie curves in Figure 5. (As noted in the methods, without scaling or normalization of amplitudes, all interaction effects or lack of interactions, are possibly confounded and not simply interpretable).

To get at the effects of primary interest here, we compared each of the Block 2 special response types with their respective pooled truth-telling/forwards-repeating values. (Since the 3-way ANOVA described above showed no differences between groups or block during truth-telling and forwards-repeating trials, the pooling was legitimate.) Thus we averaged OD1[L] and OD2-TRU to form OD-TRU, and we averaged the comparable Control data to form OD-FOW.

Within the Lie group, we then compared OD-TRU (honest) and OD2-LIE (dishonest) and examined site effects. The effect of site was F(2,22) = 89.98, pg < .001. The effect of honest vs. dishonest responses was F(1,11) = 7.11, p < .03, reflecting the lower value of averaged OD2-LIE responses in comparison with averaged OD-TRU (the pooled average of OD1[L] and OD2-TRU). The interaction of site and response type was not significant (p > .4). In the Control group, the effect of site was F(2,22) = 73.36, pg < .001. There was no significant effect of forwards versus backwards repetition (p > .2), despite the appearance of such a difference in Figure 5. Neither was the interaction of response type and site (p > .6) significant. Thus, although the dishonest response manipulation had a significant effect on unscaled P300 amplitudes in comparison with honest responses, the backwards repetition manipulation did not.

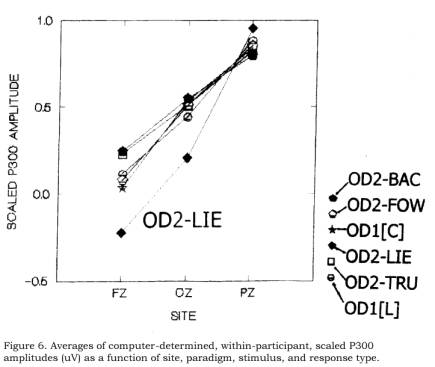
E. P300 Amplitude analysis; scaled data: group comparisons: In this section, we will comment only on interaction effects, since the scaling of data intentionally obviates main effects other than site effects, which are exaggerated (McCarthy & Wood, 1985). Figure 6 is the scaled equivalent of Figure 5, and shows scaled P300 amplitudes as a function of site, block, group, and response type. The figure suggests that all curves are similar except for the curve of the Lie group, during the second block, and only on dishonest response trials (OD2-LIE). We imply no interpretation of these scaled data which we simply here display (Figure 6) and describe (Ruchkin, Johnson, & Friedman, 1999).

Our statistical analysis approach with scaled data parallels the approach used with unscaled data. Thus the first analysis performed on scaled data was a 3-way ANOVA on all honest-responding, forward-repetition conditions, i.e., with independent variables: site, group, and block. The four response types separately submitted by group were OD1[L], OD2-TRU, OD1[C], and OD2-FOW. No interactions were expected, and none were found; (all p > .2).

Next, as with unscaled data, we combined the honest, forward response trials within each group to use as a benchmark-baseline with which to compare dishonest (Lie) or backwards (Control) responses. Thus, OD-TRU is the average of OD1[L] and OD2-TRU in the Lie group; OD-FOW is the comparable average within the Control group. Within the Lie group, a 2-way ANOVA on effect of response-type (OD-TRU vs. OD2-LIE) and site yielded a significant interaction of response type-by-site; F(2,22) = 6.76, pg < .02. Within the Control group, the comparable ANOVA on effect of OD-FOW vs. OD2-BAC with site also yielded a significant interaction; F(2,22) = 10.6, pg < .001. This was in contrast to what is suggested in Figure 6, where the scaled curves seem all alike (especially at Cz and Pz) except for the OD2-LIE (dishonest response) curve. It is noted (Figure 6), however, that whereas in the Lie group, the interaction shows (at Fz and Cz) a depression of OD2-LIE in comparison with OD2-TRU (honest vs. dishonest responses), in the control group, the OD2-BAC responses are (at Fz) slightly (though significantly) enhanced in comparison with the OD2-FOW curve. (These observations, again, imply no interpretation regarding relative activities or source strengths at the noted sites, but are meant simply to illustrate different kinds of interactions in Lie and Control groups; Ruchkin et al., 1999.)

We performed comparable ANOVAs, post-hoc, on data from just the Cz and Pz sites. In the Lie group, OD-TRU vs. OD2-LIE interacted with site, F(1,11) = 24.32, p < .001. However, in the Control group, OD-FOW vs. OD2-BAC did not interact with site (p > .15); neither did OD1-FOW vs. OD2-BAC (p > .1).

F. P300 Scaled Amplitude Analysis: Within Lie Group: The major comparison in this study is of the honest and dishonest response trials in Block 2 within the Lie group (OD2-TRU vs. OD2-LIE). This is because the task demands in the Lie group should be constant over trials within the block. A 2-way ANOVA on response type (honest/dishonest) and site did yield an interaction: F(2,22) = 7.2, pg < .02, as is evident also in Figure 6.

G. Latency Effects: Table 3 shows the Pz latencies of P300 for oddball responses in the two groups, segregated by response type. The Control group latencies are slightly greater than those of the Lie group (although the largest difference in row 1 of the table occurs prior to the group-generating manipulation). For both groups responding honestly and with forwards repetition in both paradigms, a 2-way ANOVA was performed on oddball latencies, with independent variables group and response type. There were no significant effects for group (p > .2), response type (p > .5) or interaction (p > .4).

Another 2-way ANOVA was performed on Pz latencies involving group and honest, dishonest, forwards, and backwards response types. Again there were no significant effects of group (p >.4), response type (p > .6), or interaction (p > .6). The present manipulations had no effects on P300 latencies, suggesting that stimulus processing task demands for the two groups did not differ, inasmuch as P300 latency has been associated with stimulus evaluation time (Fabiani et al., 1987; Johnson, 1988).

Table 3: P300 Pz Latencies ± SD
Lie Group		Control Group
Response Type	Latency (ms)	Response Type	Latency (ms)
OD1[L]	516 + 34.9	OD1[C]	550 +/- 53.9
OD2-TRU	518 + 80.2	OD2-FOW	528 +/- 47.3
OD2-LIE	518 + 49.6	OD2-BAC	539 +/- 44.8

Discussion

We have shown previously (Rosenfeld et al, 1998; Rosenfeld et al., 1999) that the scaled scalp distributions (profiles) of P300 amplitude in deception conditions differ from those seen in simple truth-telling conditions. Since the scaled scalp amplitude distribution is independent of amplitude itself (McCarthy & Wood, 1985; Johnson, 1988, 1993), it may well be the case that profile can become another brain-wave-based channel (dependent measure) which could be used in practical detection of deception situations. There have now been several demonstrations that P300 amplitude, itself, can be so utilized; (e.g., Rosenfeld, Cantwell, Nasman, Wojdac, Ivanov, & Mazzeri, 1988, Rosenfeld, Angell, Johnson, & Qian, 1991, Ellwanger, Rosenfeld, Sweet, & Bhat, 1996, Farwell & Donchin, 1991; Allen & Iacono, 1992.)

One could not say, however, on the basis of previous studies, that the profile seen in deceptive conditions represented neural activity specific to deception, itself, since, as reviewed in the introduction, deceptive and truth-telling conditions previously utilized also differed in task demand: the truth-teller had only to do his/her best on a simple task whereas the deceiver had to (additionally) keep track of his/her deception rate, and decide on each trial whether or not to lie.

The present study was designed to address these considerations in 2 ways: (1) allowing comparison of profiles between two groups (Lie and Control) in which we attempted to equalize task demand to the maximum possible extent, and (2) allowing comparison within the Lie group of profiles associated with honest versus dishonest response trials. Differing profiles in dishonest versus honest conditions would suggest different neurogenerator sets associated with each condition (Johnson, 1993; McCarthy & Wood, 1985). It may also be that the two conditions evoke different sets of components which differentially overlap the P300 which both conditions evoke in common (Donchin et al, 1997). In either case, however, the differing profiles indicate differing modes of brain function in each condition.

In fact, we found (Results, section F.) that scaled profiles differed in Lie group members during honest versus dishonest response trials. Since the task demand on the Lie group members was the same throughout the second paradigm task (i.e. during honest and dishonest trials), it is suggested that the significant interaction of response type (honest vs dishonest) by site provides evidence of differential modes of brain operation during the two kinds of trials, and that this effect is not confounded by task demand differences.

The Control group, like the Lie group also had to make a decision on each trial (whether or not to repeat a stimulus backwards), and had to track the same ratio of the two kinds of available responses (50-50). When scaled amplitude data from all three sites (Fz, Cz, Pz) were analyzed, this group also showed an interaction of site and response type (honest forwards repetition vs honest backwards repetition). However, the nature of the change from the forward repetition condition in the Control group was different than that seen in the Lie group. Indeed, if one considered only the Cz and Pz sites, then only the Lie group showed an interaction effect in the response type manipulation (response type x site) whereas the Control group showed no (response type x site) significant interaction. Similarly, in unscaled data from all three sites, significant main effects on amplitude were seen only in response to the honesty manipulation and not in response to the forwards vs backwards repetition manipulation. Thus the honesty-dishonesty manipulation had greater effects than the forwards-backwards manipulation (on unscaled Fz, Cz, Pz amplitudes, and on scaled profiles at Cz and Pz) in this study.

Further evidence that group differences are not attributable to stimulus complexity aspects of task demand differences comes from the latency data: The P300 latencies did not differ between Lie and Control groups. Increases in task complexity involving greater stimulus processing demand from one condition to another are usually reported to increase P300 latency (and to decrease amplitude; Johnson, 1988).

It is also the case that in a modified replication of the present experiment in which probe stimuli were randomly inserted in place of date and number stimuli, there were no differences in reaction time to these probe stimuli between Lie and Control groups. This was further evidence of the comparability of task demand in these groups. We could not look at RTs to the other stimuli (as is often customary) because of the delayed response requirement necessitated by the need to avoid vocalization artifact. The probe stimuli, however, appeared in exactly the same time slots as did the other stimuli. They were more rare and when presented, were probably unexpected, as subjects most likely anticipated presentation of dates.

It is not surprising that in scaled profile data, the Control and Lie groups had differing profiles in Block 2 in comparison with their respective benchmarks. The two tasks are quite different in two ways, involving 1) honest (Control) versus dishonest (Lie) responses, and 2) trials with forward (Lie) versus backward repetition (Control). One could not say with certainty that by themselves, these differing profiles are due to honesty differences, repetition direction differences, or both. This is why we also used a first block with all participants responding honestly with forward repetition of stimuli. Since these profile data did not differ from the honest/forward repetition data in the second block, we pooled, within each group, the honest/forward response data from both blocks and used them as baseline/benchmarks with which to compare dishonest response profiles in the Lie group and backwards response profiles in the Control group. The manipulations within each group produced different scaled profile effects, in terms of shifts from the benchmarks as noted above, and we would attribute the effect in the Lie group to effects of deception.

This is consistent with the finding of different profiles for honest and dishonest responses within the second block of the Lie group, where within one block, different profiles were obtained. These effects might be attributable to deception specifically, since, as noted above, these Lie participants were all treated alike and the only difference between the cognitive states of Lie participants on trials involving honest vs. deceptive responses is this difference in response selection.

It is noted (Figure 6) that in the Lie group, the scaled OD2-LIE (dishonest response) curve is downshifted at Cz and Fz and upshifted at Pz relative to both the honest condition of Block 1 (OD1[L]) as well as to the honest response trials of Block 2 (OD2-TRU). It is also downshifted in comparison with all Control group curves at Fz and Cz, and upshifted at Pz. (We do not here intend to interpret the interactions on scaled data in terms of loci of cortical activity responsible for the interactions, as noted in the Results section, but only mean to describe unique features of the interaction in the Lie group.) These interactions strongly suggest that the lie response has a unique effect on brain operation. The fact that unscaled amplitudes are uniquely reduced in the Lie group during dishonest responses also supports a unique attribute related specifically with dishonest responses.

A question may be raised here regarding ecological validity. Our Lie subjects were not, in fact, lying in the way people do in the field. In our instructions to them, however, we repeatedly reminded them that when they would respond as if they were making errors, that in fact, they would know very well that these were not genuine errors, but lies. (One subject actually refused to complete the study at this point and was released.) Nevertheless, it remains a limitation here that the subjects were executing directed rather than voluntary lies.

It was essential, in the design of this study, that there be no differences among the P300s associated with both blocks and groups during the honest responses. This requirement was mandated by our plan to pool honest, forwards responses so as to generate benchmark/baselines as described above. However, we also had application issues in mind: In any anticipated uses of these methods with real suspects in the field, it may be essential to have data from a control/baseline session, in which the suspect is known to be responding truthfully, with which to compare, in the same subject, data obtained during a test session in which the subject’s (dis)honesty is to be ascertained. The present results in the Lie group which showed no differences between P300 distributions associated with truthful responses from both the first and second blocks, but differences between pooled truthful responses and dishonest responses, suggest that it should be possible to develop procedures, based on current group results, for future intraindividual diagnosis.

There is another implication regarding the data obtained from both groups during honest, forwards responding: One might have predicted differences between data sets obtained from the two blocks during honest, forwards responding on the basis of the fact that the first block utilized phone numbers as stimuli, whereas the second block utilized (birth) dates. A participant might have been expected to show different scaled amplitude profiles to these two kinds of stimuli on the basis of different cognitive processing of the two classes. Such differences were not observed. (Of course, such differences might be seen in data from other scalp sites.) This negative outcome suggests that the specific nature of the stimulus does not play a significant role in determination of profile shape in the present context: Rather, an autobiographal oddball stimulus yields a typical Pz > Cz > Fz profile which does not differ as a function of the specific nature of the stimulus, so long as an honest response occurs to the stimulus. Dishonest responses, however, affect the profile. We could have counterbalanced across participants the order of stimulus class used in the present study in order to control (unobtained) effects of differing stimulus classes. We chose not to counterbalance because while this counterbalanced design would have been easily implemented in the present laboratory analog, it would appear to present major problems in intraindividual field tests.

References

Allen, J., Iacono, W.G. and Danielson, K.D. (1992). The identification of concealed memories using the event-related potential and implicit behavioral measures: A methodology for prediction in the face of individual differences. Psychophysiology, 29, 504-522.

Donchin, E., Kramer, A., & Wickens, C. 1986). Applications of brain event-related potentials to problems in engineering psychology. In M. Coles, S. Porges and E. Donchin (Eds.), Psychophysiology: systems, processes and applications. New York: Guilford.

Donchin, E., Spencer, K., & Dien (1997). The varieties of deviant experience: ERP manifestation of deviance processors in Van Boxtel, G.J.M. & Bocken, K.B.E. (Eds.), Brain and Behavior: Past, Present, and Future, Tilburg University Press, p. 116.

Fabiani, M., Gratton, G., Karis, D., & Donchin, E (1987). The definition, identification, and reliability of measurement of the P3 component of the event-related potential. In P.K. Ackles, J.R. Jennings, & M.G.H. Coles (Eds.), Advances in psychophysiology Vol. 2, Greenwich: JAI Press.

Ellwanger, J., Rosenfeld, J.P., Sweet, J.J. & Bhatt, M. (1996). Detecting simulated amnesia for autobiographical and recently learned information using the P300 event-related potential. International Journal of Psychophysiology, 23, 9-23.

Farwell, L.A., & Donchin, E. (1991). The truth will out: Interrogative polygraphy (“lie detection”) with event-related potentials. Psychophysiology, 28, 531-547.

Johnson, R., Jr. (1988). The amplitude of the P300 component of the event-related potential. in P.K. Ackles, J.R. Jennings, & M.G.H. Coles (Eds.), Advances in psychophysiology Vol. 2 (pp. 69-138). Greenwich, Ct: JAI Press.

Johnson, R. (1993). On the neural generators of the P300 component of the event-related potential. Psychophysiology, 30, 90-97.

Kramer, A.F., Sirevaag, E.J., & Braune, R. (1987). A psychological assessmentof operator workload during simulated flight missions. Human Factors, 29(2), 145-160.

Lykken, D.T. (1981). A tremor in the blood. New York: McGraw-Hill.

McCarthy, G. & Wood, C. (1985). Scalp distributions of event-related potentials: an ambiguity associated with analysis of variance models. Electroenceph. Clin. Neurophysiol., 62, 203-208.

Rosenfeld, J.P., Angell, A., Johnson, M., & Qian, J. (1991). An ERP-based, control-question lie detector analog: Algorithms for discriminating effects within individuals’ average waveforms. Psychophysiology, 38, 319-335.

Rosenfeld, J.P., Cantwell, G., Nasman, V.T., Wojdac, V., Ivanov, S., & Mazzeri, L. (1988). A modified, event-related potential-based guilty knowledge test. International Journal of Neuroscience, 24, 157-161.

Rosenfeld, J.P., Reinhart, A.M., Bhatt, M., Ellwanger, J., Gora, K., Sekera, M., & Sweet, J. (1998). P300 Correlates of simulated amnesia on a matching-to-sample task: Topographic analyses of deception vs. truth-telling responses. International Journal of Psychophysiology, 28, 233-248.

Rosenfeld, J.P. & Ellwanger, J.W. (1999). Cognitive Psycholphysiology in Detection of Malingered cognitive deficit. Forensic Neuropsychology: Fundamentals and Practice, J.J. Sweet (Ed.), Lisse, Netherlands: Swets & Zeitlinger.

Rosenfeld, J.P., Ellwanger, J.W., Nolan, K., Wu, S., Bermann, & Sweet, J.J. (1999). P300 scalp amplitude distribution as an index of deception in a simulated cognitive deficit model. Int. J. Psychophysiol., 33(1), 3-20.

Ruchkin, D.S., Johnson, R., Grafman, J., Canoune, H., & Ritter, W. (1992). Distinctions and similarities among working memory processes: an event-related potential study. Cognitive Brain Research, 1, 53-66.

Ruchkin, D.S., Johnson, R., & Friedman, D. (1999). Scaling is necessary when making comparisons between shapes of event-related potential topography. Psychophysiology, 36, 832-834.

Article submitted for publication: 14 January 2002

Revision submitted: 22 May 2002

Article accepted for publication: 8 June 2002